The Adam roller-coaster
The journey of the Adam optimizer has been quite a roller coaster. First introduced in 2014, it is, at its heart, a simple and intuitive idea: why use the same learning rate for every parameter, when we know that some surely need to be moved further and faster than others? Since the square of recent gradients tells us how much signal we’re getting for each weight, we can just divide by that to ensure even the most sluggish weights get their chance to shine. Adam takes that idea, adds on the standard approach to momentum, and (with a little tweak to keep early batches from being biased) that’s it!
When first released, the deep learning community was full of excitement after seeing charts like this one from the original paper:
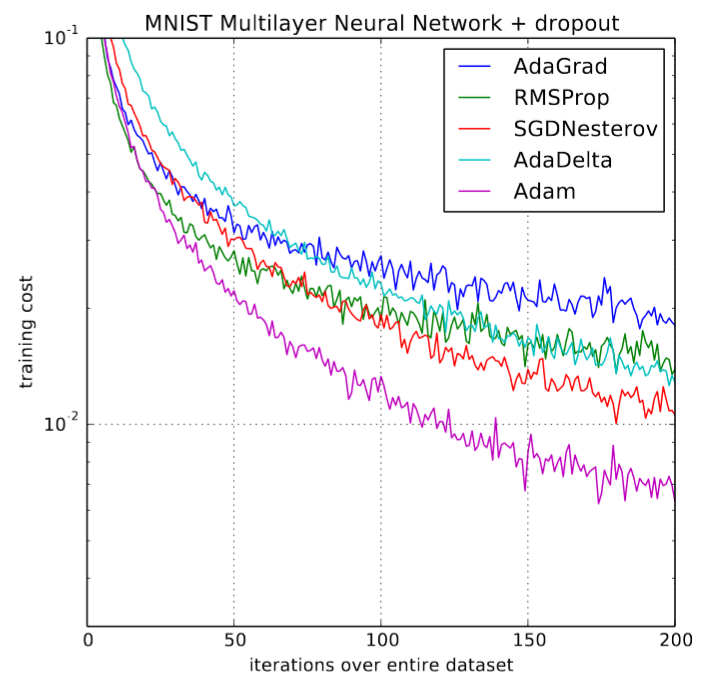
200% speed up in training! “Overall, we found Adam to be robust and well-suited to a wide range of non-convex optimization problems in the field machine learning” concluded the paper. Ah yes, those were the days, over three years ago now, a life-time in deep-learning-years. But it started to become clear that all was not as we hoped. Few research articles used it to train their models, new studies began to clearly discourage to apply it and showed on several experiments that plain ole SGD with momentum was performing better. By the time the 2018 fast.ai course had come around, the decision was made to cut poor Adam from the early lessons.
But at the end of 2017, Adam seemed to get a new lease of life. Ilya Loshchilov and Frank Hutter pointed out in their paper that the way weight decay is implemented in Adam in every library seems to be wrong, and proposed a simple way (which they call AdamW) to fix it. Although their results were slightly mixed, they did show some encouraging charts, such as this one:
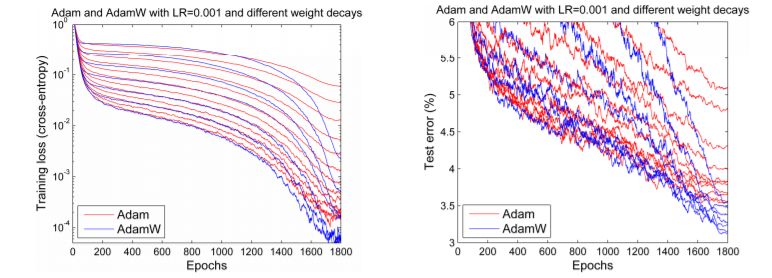
We expected to see the Adam enthusiasm return, since it seemed those first results could perhaps be found again. But that’s not what happened. Indeed, the only deep learning framework that implemented the fix was fastai, using code written by Sylvain. Without broad framework availability, day-to-day practitioners were stuck with the old, “broken” Adam.
But that’s not the only problem. More obstacles lay ahead. Two separate papers pointed out apparent problems with the convergence proof of poor Adam, although one of them claimed a fix (and won a “best paper” award at the prestigious ICLR conference), which they called amsgrad. But if we’ve learned anything from this potted history of this most dramatic life (at least, dramatic by optimizer standards), it’s that nothing is as it seems. And indeed, PhD student Jeremy Bernstein has pointed out that the claimed convergence problems are actually just signs of poorly chosen hyper-parameters, and that perhaps amsgrad won’t fix things anyway. Another PhD student, Filip Korzeniowski, showed some early results that seemed to support this discouraging view of amsgrad.
Getting off the roller-coaster
So for those of us that just want to train accurate models fast, what do we do? Let’s solve this debate the same way scientific debates have been solved for hundreds of years: with experiments! We’ll tell you all the details in just a moment, but first, here’s a summary of the results:
- Properly tuned, Adam really works! We got new state of the art results (in terms of training time) on various tasks like
- training CIFAR10 to >94% accuracy in as few as 18 epochs with Test Time Augmentation or with 30 epochs without, as in the DAWNBench competition;
- fine-tuning Resnet50 to 90% accuracy on the Cars Stanford Dataset in just 60 epochs (previous reports to the same accuracy used 600);
- training from scratch an AWD LSTM or QRNN in 90 epochs (or 1 hour and a half on a single GPU) to state-of-the-art perplexity on Wikitext-2 (previous reports used 750 for LSTMs, 500 for QRNNs).
- That means that we’ve seen (for the first time we’re aware of) super convergence using Adam! Super convergence is a phenomenon that occurs when training a neural net with high learning rates, growing for half the training. Before it was understood, training CIFAR10 to 94% accuracy took about 100 epochs.
- In contrast to previous work, we see Adam getting about as good accuracy as SGD+Momentum on every CNN image problem we’ve tried it on, as long as it’s properly tuned, and it’s nearly always a bit faster too.
- The suggestions that amsgrad are a poor “fix” are correct. We consistently found that amsgrad didn’t achieve any gain in accuracy (or other relevant metric) than plain Adam/AdamW.
When you hear people saying that Adam doesn’t generalize as well as SGD+Momentum, you’ll nearly always find that they’re choosing poor hyper-parameters for their model. Adam generally requires more regularization than SGD, so be sure to adjust your regularization hyper-parameters when switching from SGD to Adam.
Here’s an overview of the rest of this article:
AdamW
Understanding AdamW: Weight decay or L2 regularization?
L2 regularization is a classic method to reduce over-fitting, and consists in adding to the loss function the sum of the squares of all the weights of the model, multiplied by a given hyper-parameter (all equations in this article use python, numpy, and pytorch notation):
final_loss = loss + wd * all_weights.pow(2).sum() / 2…where wd is the hyper-parameter to set. This is also called weight decay, because when applying vanilla SGD it’s equivalent to updating the weight like this:
w = w - lr * w.grad - lr * wd * w(Note that the derivative of w2 with respect to w is 2w.) In this equation we see how we subtract a little portion of the weight at each step, hence the name decay.
All libraries we have looked at use the first of these forms. (In practice, it is nearly always implemented by adding wd*w to the gradients, rather than actually changing the loss function: we don’t want to add more computations by modifying the loss when there is an easier way.)
So why make a distinction between those two concepts if they are the same thing? The answer is that they are only the same thing for vanilla SGD, but as soon as we add momentum, or use a more sophisticated optimizer like Adam, L2 regularization (first equation) and weight decay (second equation) become different. In the rest of this article, when we talk about weight decay, we will always refer to this second formula (decay the weight by a little bit) and talk about L2 regularization if we want to mention the classic way.
Let’s look at SGD with momentum for instance. Using L2 regularization consists in adding wd*w to the gradients (as we saw earlier) but the gradients aren’t subtracted from the weights directly. First we compute a moving average:
moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + wd*w)…and it’s this moving average that will be multiplied by the learning rate and subtracted from w. So the part linked to the regularization that will be taken from w is lr* (1-alpha)*wd * w plus a combination of the previous weights that were already in moving_avg.
On the other hand, weight decay’s update will look like
moving_avg = alpha * moving_avg + (1-alpha) * w.grad
w = w - lr * moving_avg - lr * wd * wWe can see that the part subtracted from w linked to regularization isn’t the same in the two methods. When using the Adam optimizer, it gets even more different: in the case of L2 regularization we add this wd*w to the gradients then compute a moving average of the gradients and their squares before using both of them for the update. Whereas the weight decay method simply consists in doing the update, then subtract to each weight.
Clearly those are two different approaches. And after experimenting with this, Ilya Loshchilov and Frank Hutter suggest in their article we should use weight decay with Adam, and not the L2 regularization that classic deep learning libraries implement.
Implementing AdamW
How can we do this? Very easily if you’re using the fastai library since its implemented inside. Specifically if you use the fit function, just add the argument use_wd_sched=True:
learn.fit(lr, 1, wds=1e-4, use_wd_sched=True)If you prefer the new training API, you can use the argument wd_loss=False (for weight decay not computed in the loss) in each of your training phases:
phases = [TrainingPhase(1, optim.Adam, lr, wds=1-e4, wd_loss=False)]
learn.fit_opt_sched(phases)Here’s a quick summary of how we implemented this in fastai. Inside the step function of the optimizer, only the gradients are used to modify the parameters, the value of the parameters themselves isn’t used at all (except for the weight decay, but we will be dealing with that outside). We can then implement weight decay by simply doing it before the step of the optimizer. It still has to be done after the gradients are computed (otherwise it would impact the gradients values) so inside your training loop, you have to look for this spot.
loss.backward()
#Do the weight decay here!
optimizer.step()Of course, the optimizer should have been set with wd=0 otherwise it will do some L2 regularization, which is exactly what we don’t want right now. Now in that spot, we have to loop over all the parameters and do our little weight decay update. Your parameters should all be inside the dictionary param_groups of your optimizer, so the loop looks something like this:
loss.backward()
for group in optimizer.param_groups():
for param in group['params']:
param.data = param.data.add(-wd * group['lr'], param.data)
optimizer.step()Results of AdamW experiments: does it work?
Our first tests on computer vision problems were very encouraging. Specifically, the accuracy we managed to get in 30 epochs (which is the necessary time for SGD to get to 94% accuracy with a 1cycle policy) with Adam and L2 regularization was at 93.96% on average, going over 94% one time out of two. We consistently reached values between 94% and 94.25% with Adam and weight decay. To do this, we found the optimal value for beta2 when using a 1cycle policy was 0.99. We treated the beta1 parameter as the momentum in SGD (meaning it goes from 0.95 to 0.85 as the learning rates grow, then goes back to 0.95 when the learning rates get lower).
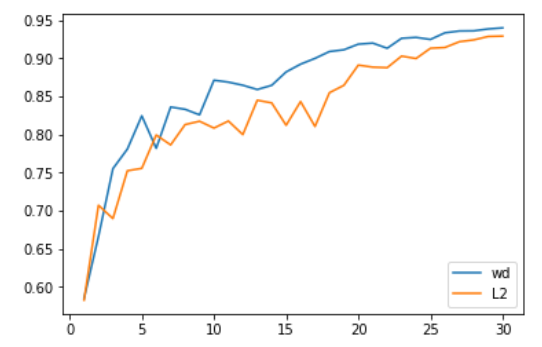
Even more impressive, using Test Time Augmentation (i.e. taking the average of the predictions on one image of the test set and four data-augmented versions of it), we can get to those 94% accuracy in just 18 epochs (93.98% on average)! With plain Adam and L2 regularization, going over the 94% happened once every twenty tries.
One thing to take into account in those comparisons is that changing the way we regularize changes the best values of weight decay or learning rate. In the tests we ran, the best learning rate with L2 regularization was 1e-6 (with a maximum learning rate of 1e-3) while 0.3 was the best value for weight decay (with a learning rate of 3e-3). The difference of orders of magnitude has been very consistent in all our tests, and comes primarily from the fact that L2 regularization gets effectively divided by the average norm of the gradients (which are pretty low) and that learning rates with Adam are pretty small (so the update of weight decay needs a stronger coefficient).
So, weight decay is always better than L2 regularization with Adam then? We haven’t found a situation where it’s significantly worse, but for either a transfer-learning problem (e.g. fine-tuning Resnet50 on Stanford cars) or RNNs, it didn’t give better results.
amsgrad
Understanding amsgrad
Amsgrad was introduced in a recent article by Sashank J. Reddi, Satyen Kale and Sanjiv Kumar. By analyzing the proof of convergence for the Adam optimizer, they spotted a mistake in the update rule that could cause the algorithm to converge to a sub-optimal point. They designed theoretical experiments that showed situations where Adam would fail and proposed a simple fix.
To understand the error and the fix, let’s have a look at the update rule of Adam (if you need a refresher, Sebastian got you covered):
avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
w = w - lr * avg_grads / sqrt(avg_squared)We’ve just skipped the bias correction (useful for the beginning of training) to focus on the important point. The error in the proof of Adam the authors spotted is that it requires the quantity
lr / sqrt(avg_squared)…which is the step we take in the direction of our average gradients, to be decreasing over training. Since the learning rate is often taken constant or decreasing (except for crazy people like us trying to obtain super-convergence), the fix the authors proposed was to force the avg_squared quantity to be increasing by adding another variable to keep track of their maximums.
Implementing amsgrad
The associated article won an award at ICLR 2018 and gained such popularity that it’s already implemented in two of the main deep learning libraries, pytorch and Keras. There is little to do except turn the option on with amsgrad=True.
This causes the weight update code from the previous section to be changed to something like this:
avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
max_squared = max(avg_squared, max_squared)
w = w - lr * avg_grads / sqrt(max_squared)Results of amsgrad experiments: a lot of noise for nothing
Amsgrad turns out to be very disappointing. In none of our experiments did we find that it helped the slightest bit, and even if it’s true that the minimum found by amsgrad is sometimes slightly lower (in terms of loss) than the one reached by Adam, the metrics (accuracy, f1 score…) always end up worse (see the tables in our introduction, or more examples here)
The proof of convergence for the Adam optimizer in deep learning (since it’s for convex problems) and the mistake they found in it mattered for synthetic experiments that have nothing to do with real-life problems. Actual tests show that when those avg_squared gradients want to decrease, it’s best for the final result to do so.
This shows that even if the focus on theory can be useful to gain some new ideas, nothing replaces experiments (and lots of them!) to make sure these ideas actually help practitioners train better models.
Appendix: Full results
Training of CIFAR10 from scratch (model is a wide resnet 22, average of the error on the test set with five models shown):
| Method | Without amsgrad | With amsgrad |
|---|---|---|
| AdamW | 5.66% | 6.31% |
| Adam | 6.06% | 6.64% |
Fine-tuning Resnet50 on the Stanford Cars dataset using the standard head introduced by the fastai library (training the head for 20 epochs before unfreezing and training with differential learning rates for 40 epochs).:
| Method | Without amsgrad | With amsgrad |
|---|---|---|
| AdamW | 10.8%/9.5% | 10.1%/9.5% |
| Adam | 10.4%/9% | 10.1%/9% |
Training an AWD LSTM with the hyper-parameters from the github repo (results show the perplexity on the validation/test set, with or without cache pointer):
| Method | Raw model | With cache pointer |
|---|---|---|
| Adam | 68.7/65.5 | 52.9/50.9 |
| Adam + amsgrad | 69.4/66.5 | 53.1/51.3 |
| AdamW | 68.9/65.7 | 52.8/50.9 |
| AdamW + amsgrad | 72.7/69 | 57/54.7 |
And the same with QRNNs instead of LSTMs:
| Method | Raw model | With cache pointer |
|---|---|---|
| Adam | 69.6/66.7 | 53.6/51.7 |
| Adam + amsgrad | 71.5/68.4 | 54.2/52.2 |
| AdamW | 70.5/67.3 | 55.5/53.3 |
| AdamW + amsgrad | 74.3/70.9 | 57.8/55.6 |
For this specific task, we used a modified version of the 1cycle policy, growing the learning rate faster, then having a long period of high constant learning rates before going down again.
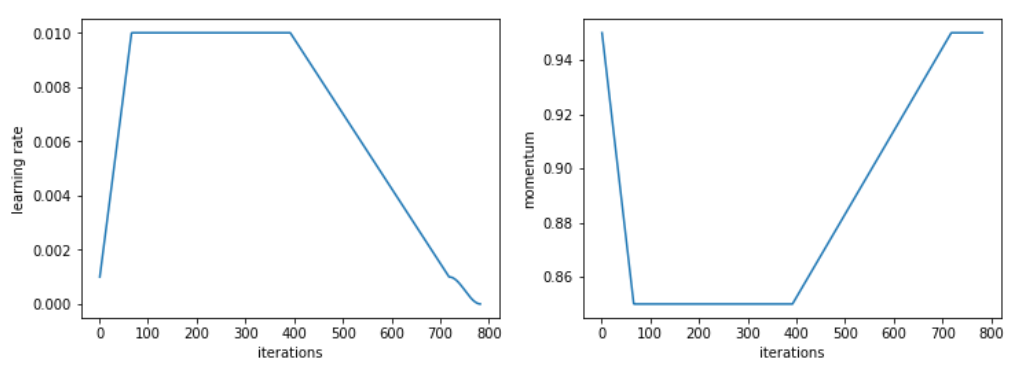
The values of all relevant hyper-parameters as well as the code used to produce these results are available here.